Dando continuidade a esta série de posts sobre alguns conceitos básicos da eletrônica, vamos falar um pouco mais sobre resistores e a Lei de Ohm.
Este conceito apesar de básico pode ajudar muito você na hora de tomar decisões sobre como seguir com seu projetos, como dimensionar resistores e outros dispositivos e a alimentação de todo o conjunto.
A Lei de Ohm
Possivelmente você já ouviu falar da Lei de Ohm nas aulas do ensino médio, em cursos de eletrônica ou talvez em buscas pela internet.
A definição da Lei de Ohm geralmente é apresentada na forma da equação (1), a qual determina que, dado um condutor ôhmico à temperatura constante, a corrente que atravessa o condutor é a razão da tensão pela resistência deste condutor.
i = V / R
(1)
Onde V é a tensão, em volts, R é a resistência, em ohms, e i é a corrente, em amperes.
Em uma definição mais textual da lei, ALEXANDER e SADIKU (2013) afirmam que “a tensão através de um resistor é diretamente proporcional à corrente fluindo por este mesmo resistor.”
A Figura 1 ilustra o fluxo da corrente convencional em um circuito simples composto pela bateria BAT1 e pelo resistor R. Nela temos V = 12 V, R = 10 Ω e consequentemente, de acordo com a equação (1), a corrente i = 1,2 A.
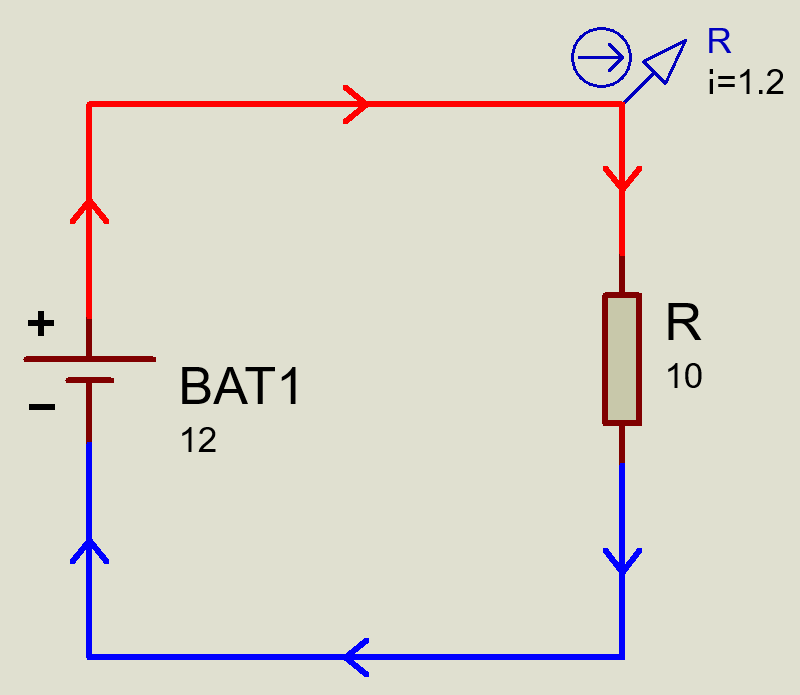
Podemos inferir, de fato, a partir da equação (1) que a corrente é diretamente proporcional à tensão e inversamente proporcional à corrente. Isso quer dizer que se a tensão V aumenta teremos um aumento proporcional na corrente e, por outro lado, se a resistência R aumenta teremos a diminuição, também proporcional, do valor da corrente.
A equação (1) pode ainda ser ser ajustada para determinar V, de acordo com a equação (2), e R, de acordo com a equação (3), dadas as devidas manipulações matemáticas simples.
V = i × R
(2)
R = V / i
(3)
Observando a Figura 1 novamente e aplicando as equações temos:
V = 1,2 × 10 = 12 V
R = 12 / 1,2 = 10 Ω
i = 12 / 10 = 1,2 A
Os resultados são exatamente os mesmos apresentados no circuito simulado da Figura 1.
Um outro olhar sobre a Lei de Ohm
Apensar de ser comum o uso da definição da Lei de Ohm como uma das equações anteriores, é preciso salientar que é uma forma minimalista de tratar o assunto, pois, segundo HALLIDAY e RESNICK (2012), a equação (2)
“[…] é usada para definir o conceito de resistência e se aplica a todos os dispositivos que conduzem corrente elétrica, mesmo aos que não obedecem à lei de Ohm. Se medimos a diferença de potencial V entre os terminais de qualquer dispositivo e a corrente i que atravessa o dispositivo ao ser submetido a essa diferença de potencial, podemos calcular a resistência do dispositivo para esse valor de V como R = V/i, mesmo que se trate de um dispositivo, como um diodo semicondutor, que não obedece à lei de Ohm“(HALLIDAY; RESNICK, 2012).
Os autores HALLIDAY e RESNICK (2012) ainda afirmam que
“Todos os materiais homogêneos, sejam eles condutores como o cobre ou semicondutores como o silício puro ou dopado com impurezas, obedecem à lei de Ohm dentro de uma faixa de valores do campo elétrico aplicado. Para valores elevados do campo elétrico, porém, sempre são observados desvios em relação à lei de Ohm.” (HALLIDAY; RESNICK, 2012).
Para ser mais direto não vamos aprofundar por este caminho de análise.
Uma breve análise de circuitos com resistores
Agora que vimos as possibilidades de associação de resistores, no post anterior, e começamos a ver as equações, podemos passar para uma breve análise.
Divisor de tensão
Vamos começar nossa análise observando o circuito da Figura 2. Na figura temos uma bateria (BAT) de 10 VCC e os resistor R1 e R2, ambos de 100 Ω. Esta configuração é a de um divisor de tensão resistivo.
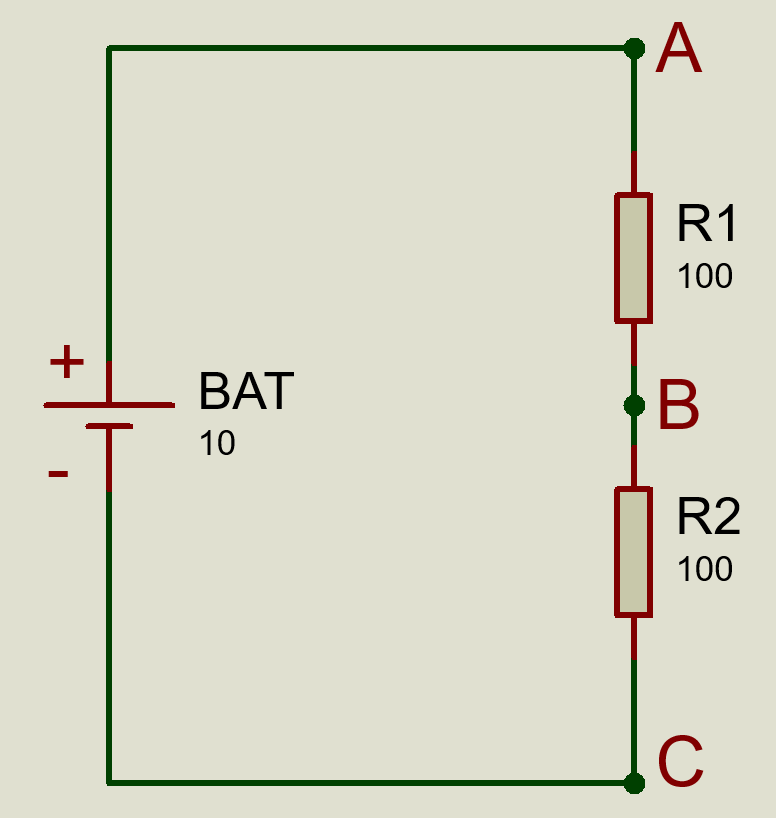
As letras A, B e C representam nós no circuito. O nó A representa o positivo da bateria, o nó B representa a junção entre os resistores R1 e R2 e o nó C representa o negativo da bateria, que é a nossa referência de zero volt ou terra (GND).
Vamos calcular qual a tensão deste circuito referente aos pontos AB, BC e AC.
Começando pelo AC, podemos ser muito diretos e afirmar que o valor da tensão de A para C é o mesmo da bateria, pois, como mencionado, o nó A está ligado ao positivo e o nó C ao negativo.
Para calcular a tensão sobre o resistor R1 (AB) ou R2 (BC), nós devemos primeiro saber qual a corrente que circula no circuito. Para isso temos que calcular o resistor equivalente (Req) da associação.
Como temos apenas dois resistores em série o Req será a soma dos dois resistores, ficando
Req = R1 + R2
Req = 100 Ω + 100 Ω
Req = 200 Ω
Agora com o valor do resistor equivalente podemos calcular a corrente usando a equação (1), utilizando o valor do resistor equivalente Req. Então temos,
i = V / Req
i = 10 / 200
i = 0,05 A = 50 mA
Esta é a corrente que flui pelo circuito como um todo.
Com esta nova informação conseguimos calcular a tensão sobre R1 (AB). Então, com a equação (2) temos:
VR1 = i × R1
VR1 = 0,05 × 100
VR1 = 5 V
Agora podemos observar que, para calcular a tensão sobre R2 (BC) teremos os mesmos valores na equação. Isso porque os resistores são de mesmo valor e a corrente é do circuito como um todo. Observe.
VR2 = i × R2
VR2 = 0,05 × 100
VR2 = 5 V
Assim podemos compreender que o circuito proposto cria um divisor de tensão resistivo com saída de 5 volts entre os nós B e nó C, ou seja sobre R2.
Este tipo de circuito pode ser utilizado para criar conversão de nível lógico para utilizarmos módulos Bluetooth com Arduino ou microcontroladores que utilizam 3,3 volts e não 5 volts como nível lógico 1.
Divisor de corrente
Nesta segunda análise vamos calcular a corrente que flui pelos resistores da Figura 3. Na figura temos três resistores, R1 de 200 Ω, R2 de 50 Ω e R3 de 60 Ω.
Nós vimos que o resistor é responsável por limitar o fluxo da corrente elétrica. Mas o quê ocorre com a corrente quando temos resistores em paralelo recebendo este fluxo?
A Figura 3 mostra que a corrente i que chega ao nó A vai se dividir entre os resistores R1 e R2 e para calcular cada parcela da corrente vamos primeiro determinar o resistor equivalente da associação.
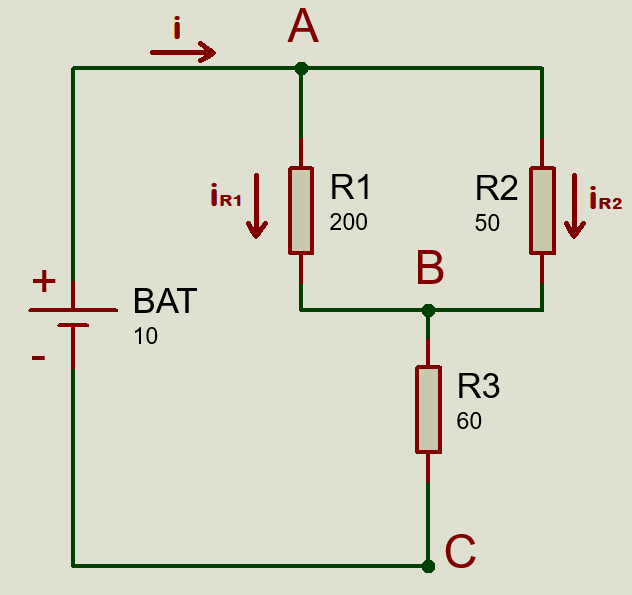
Vamos começar com o resistores em paralelo, R1 e R2. Vimos que é possível calcular o resultado de dois resistores em paralelo fazendo a razão do produto pela soma entre ambos. Considere a simbologia R1 || R2 como sendo R1 paralelo à R2.
Req12 = R1 || R2
Req12 = (200 × 50) / (200 + 50)
Req12 = 40 Ω
Dessa forma temos o resistor equivalente Req12 , refrente aos resistores R1 e R2, com valor 40 Ω.
Ainda precisamos finalizar o cálculo incluindo R3. Como R3 está em série com Req12 precisamos apenas somar os valores para, finalmente, obter o resistor equivalente de toda a associação.
Req = Req12 + R3
Req = 40 + 60
Req = 100 Ω
Seguindo como no exemplo anterior, vamos calcular a corrente total que flui pelo circuito da Figura 3.
i = V / Req
i = 10 / 100
i = 0,1 A = 100 mA
Temos então uma corrente total de 100 mA, ou 0,1 A, fluindo do nó A até o nó C.
Para encontrarmos a corrente nos resistores R1 e R2 precisamos também saber a tensão sobre eles. Como ambos estão em paralelo e ligados aos nós A e B esta tensão será a mesma para os dois.
Utilizando a Req12 podemos encontrar a tensão sobre estes resistores como a seguir.
VReq12 = i × Req12
VReq12 = 0,1 × 40
VReq12 = 4 V
Observamos então que sobre os resistores R1 e R2 temos 4 volts, ou seja,
VR1 = VR2 = VReq12 = 4 V
A partir deste ponto, para encontrar a corrente de cada um dos resistores, R1 e R2, aplicamos a equação (1) com os dados que já obtemos.
Assim,
iR1 = VR1 / R1
iR1 = 4 / 200
iR1 = 0,02 A = 20 mA ,
e ainda,
iR2 = VR2 / R2
iR2 = 4 / 50
iR2 = 0,08 A = 80 mA .
Perceba que o fluxo de corrente que atravessa cada um dos resistores é proporcional ao valor de cada um deles.
Podemos verificar que R1 é quatro vezes maior do que R2, e a corrente que atravessa R1, portanto, é quatro vezes menor que a corrente que atravessa R2. Quanto maior a resistência menor a corrente.
É preciso observar também que a soma das correntes que saem dos dois resistores é a mesma que entra. Este é um conceito chamado de Lei dos Nós, uma das leis de Kirchhoff.
Dessa forma fica fácil de afirmar que a corrente sobre R3 é simplesmente a soma das correntes de R1 e R2.
Podemos reforçar esta afirmação calculando a corrente sobre R3, apensar de ficar redundante nesta explicação. Veja.
VR3 = i × R3
VR3 = 0,1 × 60
VR3 = 6 V
e em seguida,
iR3 = VR3 / R3
iR3 = 6 / 60
iR3 = 0,1 A = 100 mA .
Aplicação
Agora que temos a noção mais básica da Lei de Ohm podemos sair um pouco da esfera puramente teórica e observar como essas equações podem nos ajudar na análise e projeto de circuitos.
Vamos começar com uma dúvida que é muito recorrente nos meus cursos de Arduino e Microcontroladores PIC. Como calcular o resistor para um LED?
Calculando o resistor para um LED
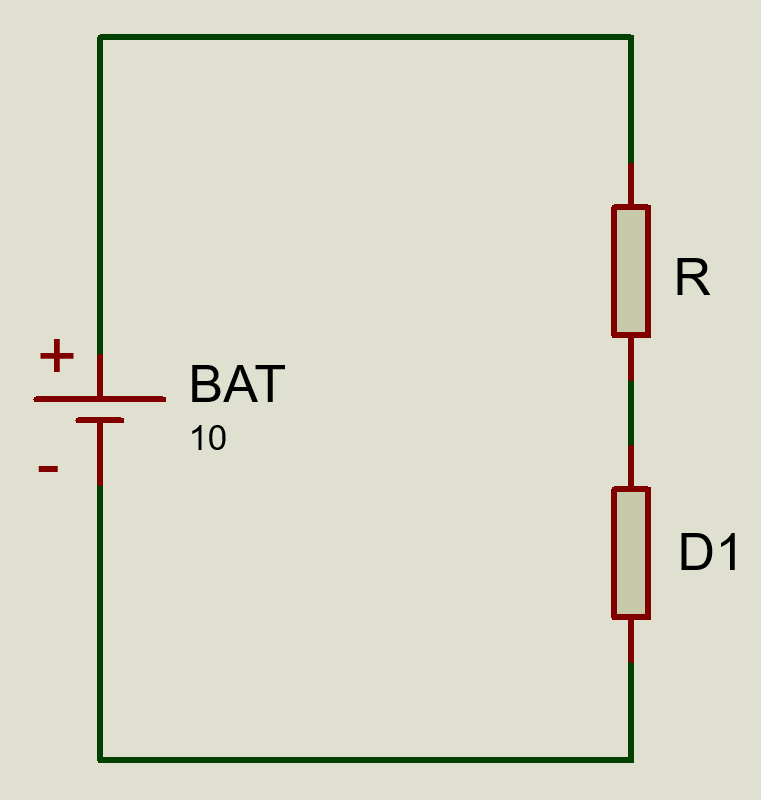
Possivelmente o circuito mais simples que você viu no início de sua jornada estudando eletrônica, seja como maker ou não, talvez seja similar ao circuito da Figura 4.
Nesta figura temos uma bateria de 10 V (BAT), um LED (D1) e um resistor R.
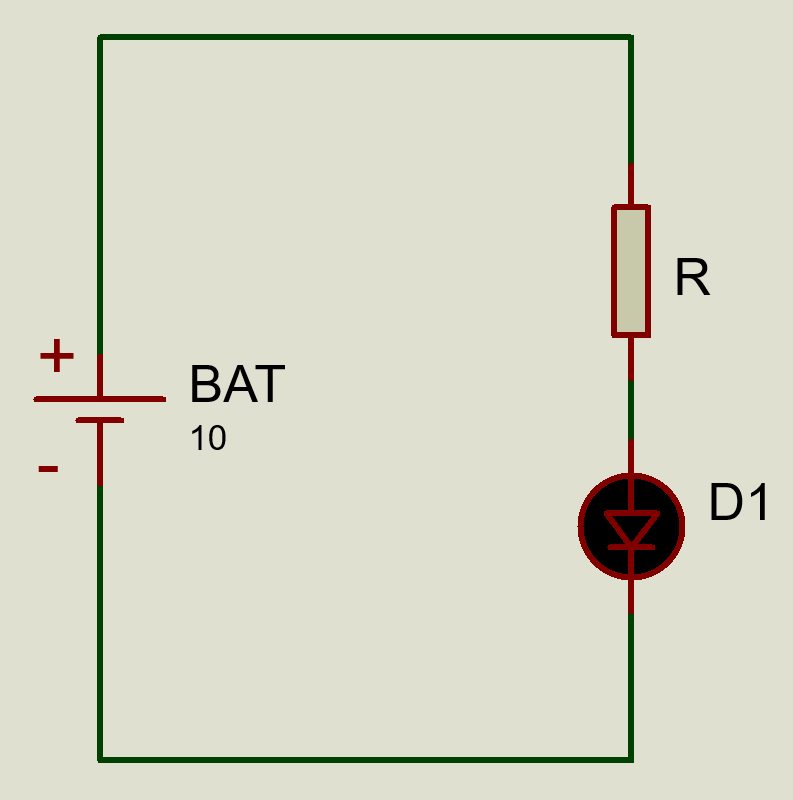
Mas afinal, qual o valor de R que deve ser utilizado para acender seguramente o LED?
Primeiro temos que ter em mente que cada componente tem suas próprias especificações e com o LED não é diferente.
Cada LED tem uma necessidade de corrente e um limite de tensão que pode ser aplicado a ele. Mesmo para LEDs de mesma cor isso pode variar com o fabricante.
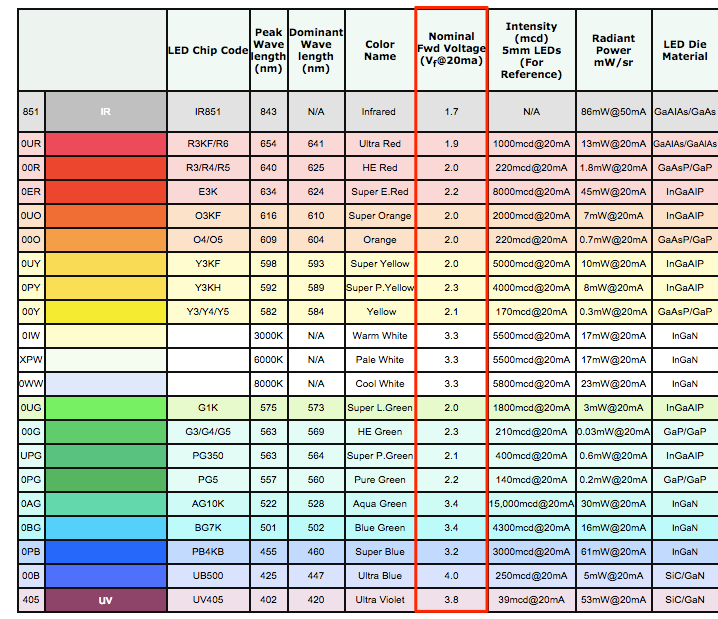
Observe a Figura 5. Nela temos informações sobre os LEDs em cada cor. A coluna destacada, Nominal Fwd Voltage (do inglês, Tensão Direta Nominal), mostra qual a tensão que deve ser utilizada com cada cor de LED. Claro que temos uma informação aproximada, pois, isso sempre pode mudar por fabricante. A tabela apresentada na Figura 5 considera que cada LED deve utilizar 20 mA de corrente.
A forma mais consistente é observar o datasheet do LED que você tem, como este apresentado na Figura 6 do datasheet em SEMICONDUCTORS (2013).

Podemos observar na Figura 6 que o LED vermelho de 5 mm deve ter uma tensão V (FORWARD VOLTAGE) típica de 2 V à 20 mA.
Como muitos compram LEDs sem saber qual o fabricante fica difícil encontrar um datasheet específico. Neste caso sugiro que utilize a referência da tabela apresentada.
No caso do nosso circuito na Figura 4 temos um LED vermelho de 5 mm. Então vamos considerar para ele 20 mA e 2 V. Isso é o que queremos para o LED, que flua 20 mA e que sobre ele tenhamos uma tensão de 2 V.
Mas vamos, por um momento esquecer que temos um LED em D1. Vamos imaginar um resistor, como na Figura 7.
Sobre este resistor imaginário queremos a tensão de 2 V com uma corrente de 20 mA fluindo.
E como calcular R agora? Precisamos saber a corrente, e sabemos, é 20 mA, e também a tensão sobre R.
Como a tensão sobre o LED, ou sobre nosso resistor imaginário, é de 2 V, o restante da tensão da fonte ficará sobre R. Assim temos sobre R uma tensão VR definida por,
VR = VBAT – VD1
VR = 10 – 2
VR = 8 V
Dessa forma conseguimos informações suficiente para calcular o valor de R com base na equação (3) da seguinte forma:
R = VR / i
R = 8 / 0,02
R = 400 Ω
Portanto, neste caso particular do nosso circuito, vamos precisar de um resistor de 400 Ω para acender nosso LED fornecendo 20 mA de corrente.
Conclusão
Neste post vimos alguns aspectos muito básicos da Lei de Ohm aplicado a resistores. O objetivo foi mostrar que com a aplicação de equações muito básicas podemos salvar nosso circuito de erros, como queimar um LED por exemplo.
Claro que o assunto é vasto e espero trazer mais informações sobre o tema em breve.
Referências
ALEXANDER, Charles K.; SADIKU, Matthew N. O. Fundamentals of Electric Circuits. 5. ed. New York, NY: McGraw-Hill, 2013. 994 p. ISBN 978-0-07-338057-5.
HALLIDAY, David; RESNICK, Robert. Fundamentos da Física, vol. 3 (Eletromagnetismo). 9. ed. Rio de Janeiro, RJ: LTC, 2012. 375 p. v. 3. ISBN 978-85-216-1905-5.
SEMICONDUCTORS, V. Vishay Semiconductors Universal LED in Ø 5 mm Tinted Diffused Package. p. 1–4, 2013.
WILKINS, Rebecca. How Many Volts are Needed to Power an LED?. [S. l.], 2015. Disponível em: https://kithub.cc/2015/11/how-many-volts-are-needed-to-power-an-led-2/. Acesso em: 10 mar. 2021.
Estudei muito esse assunto pelo livro do Haliday
Certamente um clássico! Creio que tenho o meu até hoje.